2D Physics Engine

Intro

I was originally going to make this about an angry birds clone I was making, aptly titled 'Mad Monkeys', but the physics engine ended up being far more interesting than making the game. So, here is some rambling on stuff that I learned while making the physics engine.

In this blog, I will discuss the physics behind a 2D rigid body physics engine. If you want to try out the game, here is the link to the github repo. All it is at the moment is just a level editor.

Checking for Intersection

In order to resolve collisions, we need a way to tell if two bodies are intersecting or not. For this section, we consider all polygons as convex, as those are much easier to handle than concave polygons.

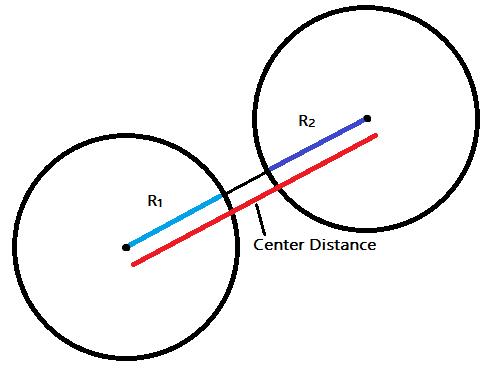
Circle vs. Circle

This is probably the simplest intersection check; you can just check if the distance between their centers is less than the sum of their radii. If it is less, then they are intersecting.

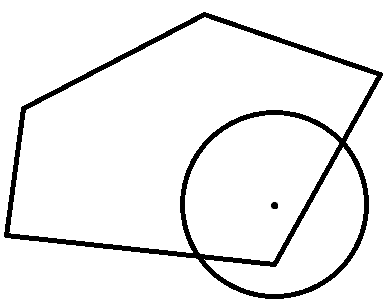
Circle vs. Polygon

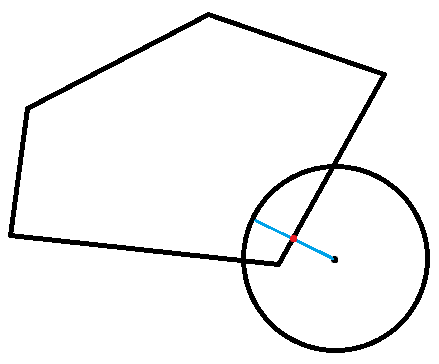
First, you can check if the center of the circle is within the polygon. If they are, then they are intersecting. Otherwise, if the circle is intersecting the polygon, it must be intersecting one of the sides. For each of the polygon's line segments, we can figure out the point on the segment that is closest to the center of the circle. If any of these points are within the circle, then we know that they are intersecting.

Polygon vs. Polygon

If two convex polygons are not intersecting, then it is always possible to draw a line where all of the points of one polygon are on one side of the line, and all of the points of the other one are on the other side. The problem now, is that how can we find this line, or declare that no such line exists given two polygons? Notice that if such a line exists, then it is also true that a line that is parallel to one of the sides of the polygons satisfies the same properties.

To test a line to see if it can separate the two polygons, we must first rotate it 90 degrees. Then, we just project all of the points onto the perpendicular line. If the two sets of points from the two polygons don't overlap, then this line can separate the two polygons. If none of the lines derived from the sides can separate the two polygons, then we consider them to be intersecting.

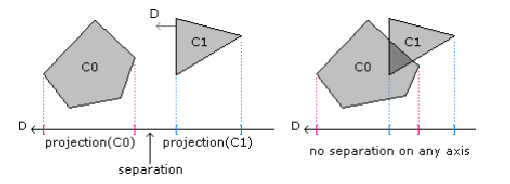
FYI, the algorithm I am describing is the GJK algorithm. It works with arbitrarily high dimensional convex shapes, and is worth looking into if you're interested.

Kinematics

Now for the physics part of the physics engine. We'll look at 1D collisions first, and then see how we can use those observations to solve 2D collisions.

1D Collisions

In your high school physics classes, you've probably learned about conservation of momentum, and conservation of kinetic energy. On top of those two, we can also add the coefficient of restitution, which is equal to the ratio of relative velocity of the two bodies before and after the collision. Essentially, restitution is just a measure of how elastic a collision is, 1 for perfectly elastic, and 0 for perfectly inelastic.

Since conservation of kinetic energy will only hold true when restitution is equal to 1, we can ignore it moving forwards. Before the collision, we know the masses of the two bodies, their corresponding velocities, and the restitution of the collision. The variables we want to solve for are the velocities of the two bodies after the collision. Since there are two equations, and two variables, this is solvable.

First, we can solve for $v_{1f}$ in the momentum equation, and $v_{2f}$ in the restitution equation, giving us: $$v_{1f} = \frac{m_1v_{1i} + m_2v_{2i} - m_2v_{2f}}{m_1}$$ $$v_{2f} = e(v_{1i} - v_{2i}) + v_{1f}$$ We can then substitute $v_{2f}$ in the first equation and solve for $v_{1f}$. $$v_{1f} = \frac{m_1v_{1i} + m_2v_{2i} - m_2e(v_{1i} - v_{2i}) - m_2v_{1f}}{m_1}$$ $$v_{1f}(1 + \frac{m_2}{m_1}) = \frac{m_1v_{1i} + m_2v_{2i} - m_2e(v_{1i} - v_{2i})}{m_1}$$ $$v_{1f} = \frac{m_1v_{1i} + m_2v_{2i} - m_2e(v_{1i} - v_{2i})}{m_1 + m_2}$$ Solving for $v_{2f}$ is a similar process that once done, gives us: $$v_{2f} = \frac{m_1v_{1i} + m_2v_{2i} + m_1e(v_{1i} - v_{2i})}{m_1 + m_2}$$

Notice that we remove the absolute value signs from the restitution equation. We can do this because we won't consider the case where the right side of the equation resolves to negative, since that would indicate a situation where the two bodies phase through each other, for example, a bullet passing through a sheet of wood.

1D Impulse

When resolving collisions, it's nice to figure out the force of the collision. That way, if we know the force, $f$, we can just apply it onto both objects within our physics world, and the collision is resolved. But the problem here is that we are dealing with rigid bodies that are infinitely hard, which means that the time, $t$, of the collision is 0. Since change in momentum is equal to $ft$, this implies that $f$ has to have infinite magnitude, and that's a problem.

We can get around this by just directly calculating the expected change in momentum, or impulse, that the collision will have on the two objects. Since momentum is just velocity times mass, and we know both the initial and final velocities, we already know impulse.

$$\text{Impulse}(m_1) = m_1v_{1f} - m_1v_{1i}$$ $$= m_1(\frac{m_1v_{1i} + m_2v_{2i} - m_2e(v_{1i} - v_{2i})}{m_1 + m_2} - v_{1i})$$ $$= m_1(\frac{m_1v_{1i} + m_2v_{2i} - m_2e(v_{1i} - v_{2i}) - m_1v_{1i} - m_2v_{1i}}{m_1 + m_2})$$ $$= m_1(\frac{m_2v_{2i} - m_2v_{1i} - m_2e(v_{1i} - v_{2i})}{m_1 + m_2})$$ $$= m_1m_2(\frac{v_{2i} - v_{1i} - ev_{1i} + ev_{2i}}{m_1 + m_2})$$ $$= \frac{m_1m_2}{m_1 + m_2}(1 + e)(v_{2i} - v_{1i})$$ $$= \frac{(1 + e)(v_{2i} - v_{1i})}{\frac{1}{m_1} + \frac{1}{m_2}}$$

To find impulse for $m_2$, we can just negate the impulse for $m_1$, due to Newton's third law.

2D Collisions

Now, how will this help us solve 2D collisions? The crucial observation to solving 2D collisions is to notice that they are just 1D collisions in disguise. When two bodies collide in 2D, any velocity that is perpendicular to the surface normal of the collision is unaffected, and we can treat the collision like a 1D collision with just the components of velocity that are normal to the collision surface.

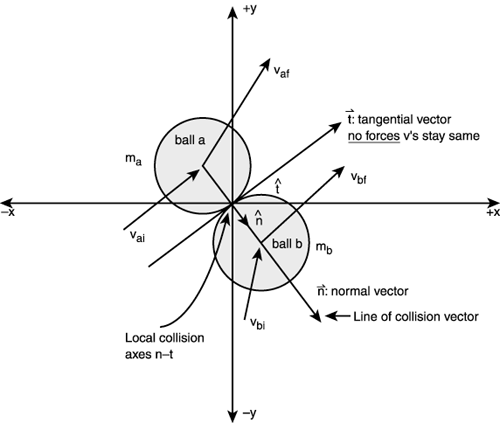
To find the component of velocity that is normal to the surface, we can simply project the velocity vector onto the surface normal vector. Subtracting the normal component of the velocity vector from the velocity will give us the tangent component.

Angular Momentum

But what if the surface normal is not directly facing the center of mass of the object being hit? In this case, the impulse generated by the collision will apply a torque onto the body. The magnitude of this torque is equal to the cross product between the impulse vector, and the vector pointing from the center of mass to the contact point.

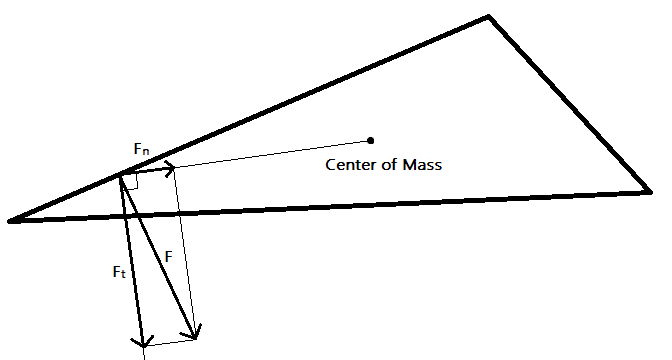
In order to find the magnitude of the impulse, we first must know the relative velocity between the two contact points before the collision. This can be found using some linear algebra: $$\text{Relative Velocity(}\vec{r}\text{)} = \vec{v_{2i}} + (\perp\vec{r_2}) \omega_2 - \vec{v_{1i}} + (\perp\vec{r_1}) \omega_1$$ $r_1$ and $r_2$ are the vectors pointing from the centers of masses of the bodies to the contact points, $c_1$ and $c_2$. $\omega_1$ and $\omega_2$ are the angular velocities of the bodies.

Next, since we know the restitution of the collision, we can directly calculate the total amount of impulse force, half of which will go to each of the colliding bodies. $$\text{Impulse} = \frac{(1 + e) * \vec{r}}{\frac{1}{m_1} + \frac{1}{m_2} + \frac{(\vec{r_1} \times \vec{n})^2}{I_1} + \frac{(\vec{r_2} \times \vec{n})^2}{I_2}}$$ $I$ is the moment of inertia, and $n$ is the surface normal vector.

Once we have the magnitude of impulse, we can apply it to the bodies at the point of contact. When applying the force, make sure to separate it into one component that will affect linear momentum, and one component that will apply torque.

Friction

When computing the magnitude of impulse due to friction, we can use the component of velocity that is tangent to the surface normal. Remember that the formula for the force of friction is: $$\mu N$$ where $\mu$ is the static or kinetic coefficient of friction, depending on whether the relative tangent velocity is non-zero, and $N$ the normal force, which is the impulse force of the collision.

Applying the impulse due to friction is the exact same process as applying the impulse due to the rest of the collision.

Convex Partitioning

If you wanted to have concave polygons in your physics engine, the easiest way to do so is to use multiple convex polygons to represent one concave one, or in other words, create a convex partition of a concave polygon. This works well if you can manually partition your concave polygons, but what sort of algorithms are there to generate convex partitions of concave polygons if, for example, you want to procedurally generate polygons to put into your physics scene?

Polygon Triangulation

To start, we can try to split our polygons into triangles. Triangles are nice because they are guaranteed to be convex, and splitting a polygon into triangles is relatively simple. One method is the 'ear clipping' method, where we can remove the ears off of the polygon until there are none left.

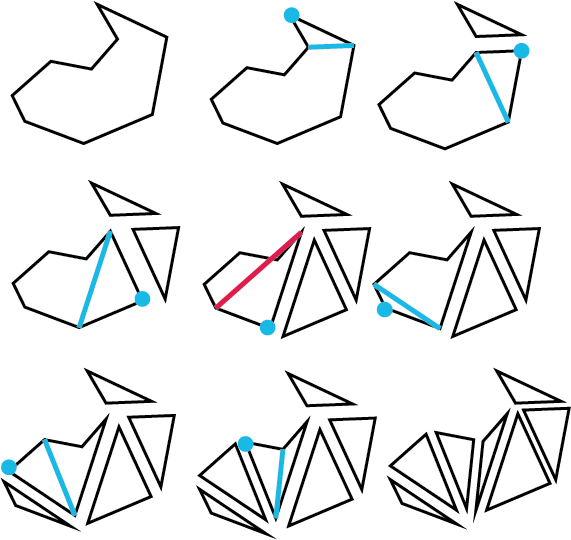
Other methods of triangulation involve first partitioning the polygon into one or more monotone polygons, and then using a linear time algorithm to partition each of those into triangles. Although these other methods might be much faster, the ear clipping algorithm is usually fast enough to where it won't be the bottleneck when you still have to do physics updates on the generated polygons.

Generating Convex Partitions

Once you have the triangle partition for a polygon, we can easily generate a convex partition. All we have to do is to pick one triangle that hasn't been used yet, making this our current convex polygon, then greedily union other unused triangles with our current polygon, as long as the resulting polygon is still convex. When there are either no more triangles left to add, or adding another triangle will always make the current polygon concave, then we add the current polygon to the partition, and pick another unused triangle to start. It has been shown that this method of creating convex partitions will never produce more than four times the minimum amount of convex polygons needed to partition the original polygon.

Limitations

Note that the above methods only work for simple polygons; polygons that don't intersect themselves and have no holes. In order to generate a triangulation for polygons with holes, you must use the monotonic polygon partition method, but the greedy triangle union method for generating a convex partition from triangles still works.